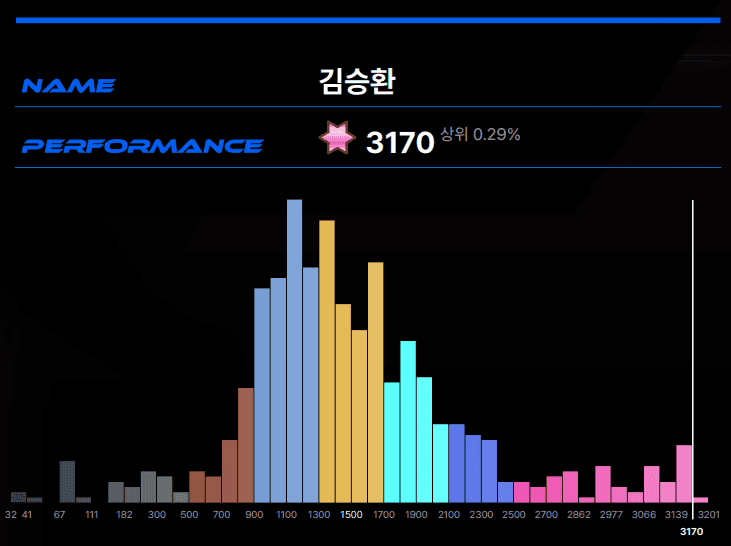
I participated in NYPC Code Battle 2025, placing 2nd in the preliminary round and advancing to the finals. Shout-out to my teammate, Donghyeon Kang (aren227).
It was a strategy competition for a virtual board game, reminiscent of the old-fashioned AI competition. Due to file size limitations, the competition centered on statistics, game theory, and algorithms rather than neural networks.
It was a fun and unique contest. I hope Nexon continues to host contests like this.
For those who are curious about our strategy, I’m leaving some points.
An optimal strategy exists when the goal is to maximize the difference in expected scores. What complicates the problem is that there are auctions for each set of dice, and . Considering the rule of score return, the problem becomes simpler when we treat the bid for as a negative bid. Then let be the expected score when player takes dice set and vice versa. Bidding is the Nash equilibrium and therefore optimal.
Expected values can be preprocessed in a feasible time via dynamic programming. DP[bitmask for rules used][dice set held][total base score] can express entire states of single player. The main challenge lies in the transition, since the cost of choosing one of the two sampled dice sets varies depending on the bids of both players. Interestingly, assuming both players follow the optimal strategy, this can be simplified to merely taking a single random dice set. The proof, briefly written, is as follows:
All that remains is a lot of implementation, which can even be parallelized.
Beyond expected value, consider the distribution of scores. If both players follow the strategy that maximizes expected value, the game is decided entirely by luck. How can we overcome this? When ahead, a player should play conservatively to avoid giving the opponent any leverage, even if it means taking a small loss. When behind, a player should take risks to win big. However, modeling the full distribution, or even just its variance, is extremely expensive. Our team used several heuristics for it.
The mid-contest evaluations are unreliable. The results were based on a Bo1 Swiss system due to cost. Since luck is crucial in this game, a single round provides little information. We evaluated strategies locally based on a round-robin with thousands of matches.
It is VERY effective to keep as much information in the preprocessed DP table as possible. Many teams have likely truncated the information of the table due to file size limitations. But, increasing the quantization bit by one yielded the greater win rate than all the heuristics we tried. We used LZMA compression, shuffled the table dimensions, post-processed the values, and ultimately scrambled all indices into a format favored by the compression algorithm, which is completely uninterpretable to humans. These measures increased our quantization precision by 4 bits.